如何求高中函数的最大值和最小值?函数的最大值分为函数的最小值和函数的最大值。如何求函数的最小值?如何求函数的最大值和最小值?如何求函数的最大值和最小值?求函数最大值的常用方法是乘积法,如何求一个二次函数的最小值?函数的最大(最小)值的几何意义函数图像的最高(低)点的纵坐标就是函数的最大(最小)值。

1、如何求函数f(x,y
假设二元函数f(x,y)的稳定点为(x0,y0),即f (x0,y0)/xf (x0,y0)/y0;注:af(x0,y0)/xbf (x0,y0)/xycf (x0,y0)/yacb if: > 0 (1) a0,f(x0,y0)为最小值;如果:0,
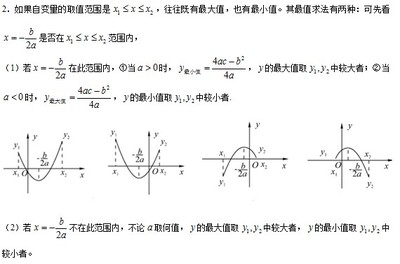
有一个最大值。最大值为(4acb)/(4a)。如果我帮助你,给我一个好的评价。看二次项的系数。如果二次项的系数大于0,则存在最小值,最小值就是顶点值。如果二次项的系数小于0,则存在最大值,最大值就是顶点值。让yaxbxc,(a ≠ 0,下同)yaxbxca (xbx/a (b/4a)昌化班吉焦帮邪爆矛78;))CB/(4a) a (x (b/2a)) (4acb)/(4a)因此,

2、高中函数的最大值和最小值怎么求
一般来说,函数的最大值分为函数的最小值和函数的最大值。简单来说,最小值就是函数在定义域中的最小值,最大值就是函数在定义域中的最大值。函数的最大(最小)值的几何意义函数图像的最高(低)点的纵坐标就是函数的最大(最小)值。求最大值的常用方法1。匹配法:形状的函数,根据二次函数的极值点或边界点的值确定函数的最大值。2.判别式法:形式为的分式函数,它被转化为系数为y的关于x的二次方程..

3.利用函数的单调性:首先定义函数的定义域和单调性,然后求最大值。4.利用均值不等式、形函数和≥≤,注意正、定等的应用条件。,即A和B是否为正数且为定值,ab的等号是否成立。5.代入法:形式为的函数,使x可以反求,然后代入上式就可以得到关于t的函数。注意t的定义域的范围,然后求关于t的函数的最大值..还有三角换元法和参数换元法。6.数形结合法形:如果把公式的左边看成一个函数,右边看成一个函数,把它们的图像做在同一个坐标系中,观察它们的位置关系,运用解析几何知识求最大值。
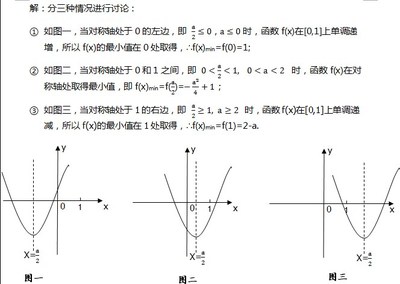
3、如何求函数的最大值和最小值?
先求导,然后让导数等于0得到可能的极值点,再通过判断导数的正负来判断单调性,最后得到极值,再计算端点值。比较大小,最大的是最大的,最小的是最小的。不是所有的函数都有导数,一个函数也不一定在所有点上都有导数。如果函数的导数存在于某一点,就说它在这一点上是导数,否则就叫非导数。但是,可导函数必须是连续的;不连续函数必须是不可微的。
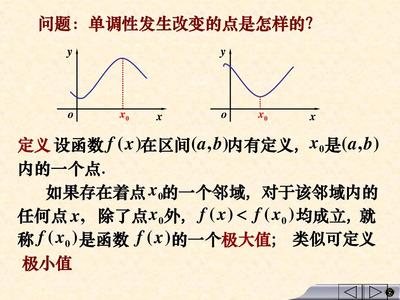
求已知函数在某一点的导数或其导函数的过程称为求导。扩展数据:极值是函数的最大值或最小值。如果一个函数在一个点的邻域内处处都有某个值,并且该点的值是最大值(最小值),那么这个函数在该点的值就是最大值(最小值)。如果大于(小于)邻域内其他点的函数值,则为严格最大值(小于)。这个点相应地被称为极值点或严格极值点。

4、函数的最大值和最小值怎么求
1。求函数最大值最常用的方法是生产、科研和日常生活中经常遇到的一类特殊的数学问题。是高中数学的一个重点,涉及高中数学知识的方方面面。解决这类问题,往往需要综合运用各种技巧,灵活选择合理的解题方式,但教材中并没有系统的描述。所以在数学总复习中,通过例题和习题的分析,

转化为一个系数为y的关于x的二次方程,因为∴≥0,求y的最大值容易产生根,所以在求最大值时需要检验x的对应值是否有解。3.利用函数的单调性,先明确函数的定义域和单调性,再求最大值。4.利用均值不等式,形式函数,和≥≤,注意正确性。
5、怎么 求函数的最小值?
求x1的绝对值加上x2的绝对值,直到达到x2014的最小值。当n为奇数,X取(n-1)/2时,x1,x2,Xn的绝对值大于或等于| (x1) (x2)…(x (n1)/2) (n3)/2x)…(N。
