折腾除法折腾除法,折腾除法,什么是C语言中的折腾除法用折腾除法(欧几里德算法)求两个正整数的最大公约数。折腾的分工是什么?折腾的分工是什么?交替除法的最大用途是求两个数的最大公约数,相除是求两个数的最大公约数的方法,是求最大公约数的算法,转与转的除法最早出现在欧几里得的《几何原本》(第七卷。
1、如何用辗转相除法求两个数的最小公倍数(步骤
在数学中,轮流除法又称为欧几里德算法,是一种求最大公约数的算法。轮流除法最早出现在欧几里得的《几何原本》(第七卷,命题一、命题二),但在中国可以追溯到九章算术,出现在东汉。两个整数的最大公约数就是能同时整除的最大正整数。轮流划分的依据如下。

所以147和105的最大公约数也是21。在这个过程中,较大的数减少,所以继续同样的计算可以不断减少这两个数,直到其中一个变为零。这时剩下的还没有变成零的数就是两个数的最大公约数。也可以用除法导出,两个数的最大公约数可以用两个数的整数倍相加来表示,比如215× 105。
2、请问什么是辗转相处除法??
过渡除法过渡除法又称为Euclideanalgorithm,是一种求两个正整数的最大公因数的算法。它是已知最古老的算法,可以追溯到3000年前。最早出现在欧几里得的《几何原本》(第七卷,命题一、命题二),而在中国则可以追溯到《九章算术》,出现在东汉时期。它不需要将两个数分解成质因数。证明:设两个数为A和B (B < A),求它们的最大公约数(A和B)的步骤如下:A除以B得A = BQ…R1 (0 ≤ R)。

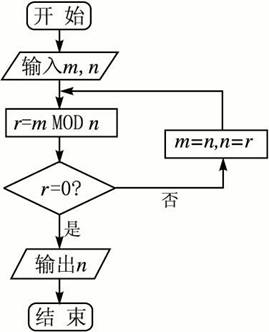
这样下去,直到它被整除。它的最后一个非零余数是(a,b)。用折腾除法求两个正整数的最大公约数(欧几里德算法)。解析:设两个数m,n,设m>n,将m除以n,得到余数q,若q为0,则m为最大公约数;如果q不等于0,则进行如下迭代:mn,nq,即原除数变成新被除数,原余数变成新除数,重复算法直到余数为0。余数为0时的除数n是原m和n的最大公约数。

3、辗转相除法是什么
多相减法,或称“相除法”,用于求最大公约数。给两个正整数A和B,A除以B得到商a0和余数R,写出公式:aa0b r,0 ≤ R < B………..(1).这是最基本的公式。如果R等于0,那么B可以除A,而A,R .余数r1,即ba1r1,0 ≤ r1 < r………….(2)如果r10,那么R除B,(1)也除A,所以R是A和B的公约数,反之,任何一个除A和B的数都被(1)除,所以R是A和B的最大公约数,0 ≤ r2 < r1…………(3)如果r20,那么(2)说明r1是B和R的公约数,而(1)中,r1也是A和B的公约数,反过来,如果一个数被A和B除,那么(1)它一定被B和R除,(2)它

4、辗转相除法例子
轮流除法最大的目的是求两个数的最大公约数。用(a,b)来表示a和b的最大公约数,有一个定理:已知a和c是正整数,如果a除以b,c剩余,则(a,b)(b,c)。例:求15750和27216的最大公约数。求两个数的最大公约数的步骤如下:首先将一个小数除以一个大数,得到第一个余数;将一个小数字除以第一个余数,得到第二个余数;将第一余数除以第二余数以获得第三余数;这样就用最后一个数除以前面的余数,直到余数为0。
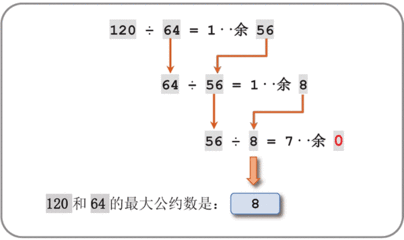
比如求1515和600的最大公约数,第一次:1515除以600,商2是315;第二遍:600除以315,商是1和285;第三遍:315除以285,商是1和30;第四遍:285除以30,商是9和15;第五遍:30除以15,商是2和0。1515和600的最大公约数是15,相除是求两个数的最大公约数的方法。
